تبدیل مبناهای ریاضیاتی
در این بخش آسان ترین راه تبدیل مبناهای ریاضیاتی و انواع سیگنالهای اطلاعاتی را بررسی کنیم .
مبناهای ریاضیاتی : به اعدادی پایه ای گفته میشود که میتوان از 0 تا بی نهایت را با آنها بیان کرد.
مبناها در واقع حروف الفبای ریاضیات هسنتد . یعنی هر عددی را بیان کنید . از یک سری رقم تشکیل شده است . مانند 0 تا 9 در زبان انسان.
انواع مبناهای ریاضیاتی :
- باینری (مبنای 2 یا دو دویی)
- اکتال (مبنای 8)
- دسیمال (مبنای 10 یا ده دهی)
- هگزا دسیمال (مبنای 16) :
باینری زبان ماشین است و در کامپیوتر و دستگاههای دیجیتال استفاده میشوند.ودسیمال یا مبنای ده زبان انسان است.
باینری (مبنای 2 یا دو دویی) :این مبنا برای بیان اعداد تنها از دو رقم 0 و 1 استفاده میکند .
اکتال (مبنای 8): دارای هشت رقم پایه میباشد ( 0 تا 7).
دسیمال (مبنای 10 یا ده دهی) : دارای ده رقم پایه است. یعنی از 0 تا 9 .زبان انسان دسیمال است.
هگزا دسیمال (مبنای 16) : دارای 16 رقم پایه است. یعنی از 0 تا 15 بصورت زیر :
0-1-2-3-4-5-6-7-8-9-a-b-c-d-e-f
a معادل عدد 10 و b=11 و …. f=15.
همانطور که می بینید از ده تا پانزده با حروف الفبای انگلیسی مشخص میشود.
هگزا دسیمال برای بیان اعداد بزرگ کاربرد دارد . در علومی مانند نجوم و علم نانو از هگزا دسیمال استفاده میشود .
انواع سیگنالهای اطلاعاتی
سیگنال چیست : سیگنال در بر دارنده اطلاعات الکترونیکی نشانه گذاری شده است. سیگنالها برای انتقال اطلاعات از دستگاه ها استفاده میشود و حاوی یک سری اطلاعات میباشد.
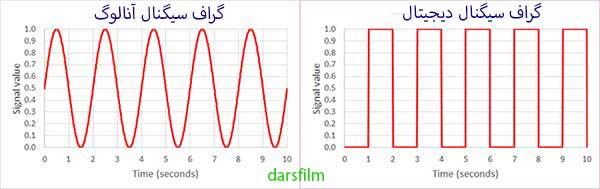
سیگنال بر دو نوع است : انالوگ و دیجیتال (رقمی )
- انالوگ(پیوسته): سیگنالهای آنالوگ قدیمی تر است .استفاده از این سیگنالها امروز کمتر و محدوده تر شده است . تلفنهای قدیمی ، ویدیوها ، تلویزیونهای قدیمی و .. عموما آنالوگ بودند.
- Digital(گسسته) رقمی : امروزه سیگنالهای اطلاعاتی در دستگاههای دیجیتال بصورت باینری (دودویی- 0 و 1 – رقمی ) هستند . و اکثر دستگاههای الکترونیکی برای انتقال اطلاعات از این نوع سیگنال استفاده میکنند . دوربینها ، تلویزیونها ، تلفنها و … امروزه از سییگنال دیجیتال استفاده میکنند .
عبارت digit به معنای رقم و دیجیتال به معنای رقمی است .
آسان ترین راه تبدیل مبناهای ریاضیاتی:
تبدیل عدد از مبنای دو یا باینری به مبنای ده یا دسیمال
نکته : جدول سلسله اعداد باینری از سمت راست و از عدد یک شروع میشود و هر بار دو برابر میشود . 1-2-4-8-16-32-64-و …
سوال : عدد 10110 را از مبنای دو یا باینری به مبنای ده یا دسیمال ببرید.
مرحله اول : سلسه اعداد باینری را به تعداد رقمهای عددی که میخواهیم به مبنای دو ببریم رسم میکنیم .
پس نیاز به یک جدول 5 ستونی داریم .
| 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 |
مرحله دوم : مانند جدول فوق عددی که میخواهیم به مبنای ده ببریم را به ترتیب زیر جدول فرار می دهیم .
مرحله سوم : خانه هایی که در زیر آنها عدد یک ذکر شده را با هم جمع می کنیم .
16+4+2=22
پس نتیجه می گیریم : عدد 10110 در مبنای 2 برابر است با عدد 22 در مبنای ده.
تبدیل عدد از مبنای 10 یا دسیمال به مبنای 2 یا باینری
سوال : عدد 42 را از مبنای ده یا دسیمال به مبنای 2 یا باینری ببرید .
در این مثال میخواهیم بدانیم اگر کامپیوترمان بخواهد عدد 42 را عنوان کند .آن را به چه شکل بیان کند .
مرحله اول : ابتدا جدول اعداد باینری را رسم می کنیم . آن را تا جایی ادامه میدهیم که به عددی مساوی یا بزرگتر از عدد مورد نظر(42) برسیم .جدول زیر :
| 1 | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|
برای درک بهتر موضوع به توضیح زیر دقت کنید .
در این مثال فرض کنید یک ظرف 42 لیتری در دست دارید و چند ظرف 64،32،16،8،4،2،1 بر روی میز کار مقابلتان . حالا شما با ظرف 42 لیتری که در دست دارید باید ظرفهای مقابلتان را پر کنید . این ظروف یا باید کاملا پر شوند یا خالی بمانند . هر ظرفی را پر کردید طبیعتا به همان اندازه از ظرفیت 42 لیترتان کاسته میشود .
مرحله دوم : عدد مورد نظر(42) را از سمت چپ به ترتیب داخل خانه ای که از عددمان کوچکتر است می ریزیم.(محتوای خانه ای که از عدد مورد نظر بزرگتر است صفر و خانه ای که کوچکتر است 1 می شود .
مرحله سوم : مرحله دوم را تا آخر با بافیمانده عدد انجام میدهیم .
توجه : در این روش عدد را در خانه ای که ظرفیت آن از عدد مورد نظر کوچکتر است میریزیم و باقیمانده را محاسبه میکنیم .مثلا اینجا 64 بزرگتر است و نمیتوانیم عدد 42 را در آن بریزیم و آن را کاملا پر کنیم پس خانه 64 خالی میماند .
| 1 | 2 | 4 | 8 | 16 | 32 | 64 |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| باقیمانده 0 | باقیمانده 0 | باقیمانده 2 | باقیمانده 2 | باقیمانده 10 | باقیمانده 10 | باقیمانده 42 |
در زیر جدول عدد 0101010 را داریم از آنجایی که صفر پشت عدد خوانده نمیشود صفر سمت چپ را حدف میکنیم .
نتیجه :
42=101010
نکته : روش دیگر این محاسبه استفاده از تقسیمهای متوالی است . در این روش به صورت زیر عمل می کنیم .
تبدیل مبناهای ریاضیاتی روش تقسیمهای متوای
تبدیل اعداد از مبنای 2 به مبنای 10:
ابتدا باید اعداد دودویی را به صورت اعداد دهگانی تبدیل کنیم. برای این کار، باید هر رقم دودویی را با توان 2 به توان مربوطه آن رقم ضرب کرده و سپس حاصل را با سایر اعداد دودویی مرتبط با آن اعداد دهگانی جمع کنیم. به عنوان مثال، برای تبدیل عدد دودویی 1011 به عدد دهگانی، باید به صورت زیر عمل کنید: 1 2^3 + 0 2^2 + 1 2^1 + 1 2^0 = 8 + 0 + 2 + 1 = 11 بنابراین، عدد دودویی 1011، معادل با عدد دهگانی 11 است.
تبدیل اعداد از مبنای 10 به مبنای 2:
ابتدا عدد دهگانی مورد نظر را به صورت باینری تبدیل کنید. برای این کار، باید به توالی از باقیماندهها و تقسیمات بخشهای متوالی عدد دهگانی به 2، توجه کنید. در هر مرحله، با تقسیم عدد دهگانی به 2، یک باقیمانده به دست میآید که این باقیمانده معمولاً 0 یا 1 خواهد بود. سپس، تقسیم دهگانی را بر 2 کرده و نتیجه را به صورت صحیح به مرحله بعدی انتقال میدهیم. این روند را تا زمانی که عدد دهگانی به 0 برسد، ادامه میدهیم. سپس، باقیماندههای به دست آمده را به ترتیب از پایین به بالا قرار داده و به عنوان عدد دودویی به دست میآوریم. به عنوان مثال، برای تبدیل عدد دهگانی 23 به عدد دودویی، باید به صورت زیر عمل کنید:
23 / 2 = 11 1 11 / 2 = 5 1 5 / 2 = 2 1 2 / 2 = 1 0 1 / 2 = 0 1
بنابراین، عدد دهگانی 23، معادل با عدد دودویی 10111 است



