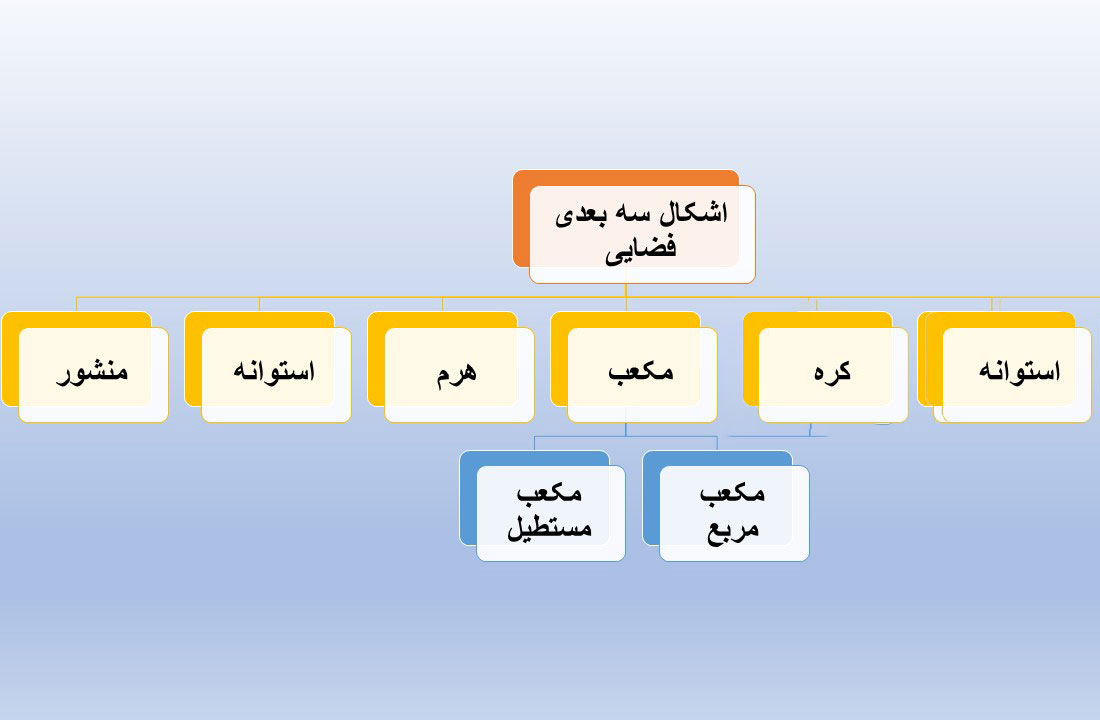
محیط و مساحت اشکال سه بعدی یا فضایی
در ادامه بحث اشکال به محیط و مساحت اشکال سه بعدی یا فضایی می پردازیم ابتدا :
🔷 اشکال هندسی سهبعدی (فضایی)
📌 تعریف و ویژگیهای کلیدی
اشکال سهبعدی به اجسامی گفته میشود که:
- دارای طول، عرض و ارتفاع هستند
- حجم را اشغال میکنند
- از ترکیب اشکال دوبعدی در فضا تشکیل میشوند
- در زندگی روزمره کاربردهای فراوان دارند
🏗️ عناصر اصلی اشکال سهبعدی
- وجه (Face): سطوح تخت یا منحنی
- یال (Edge): خطوط تقاطع وجوه
- رأس (Vertex): نقاط اتصال یالها
- محور (Axis): خطوط تقارن
محیط و مساحت تمام اشکال سه بعدی یا فضایی
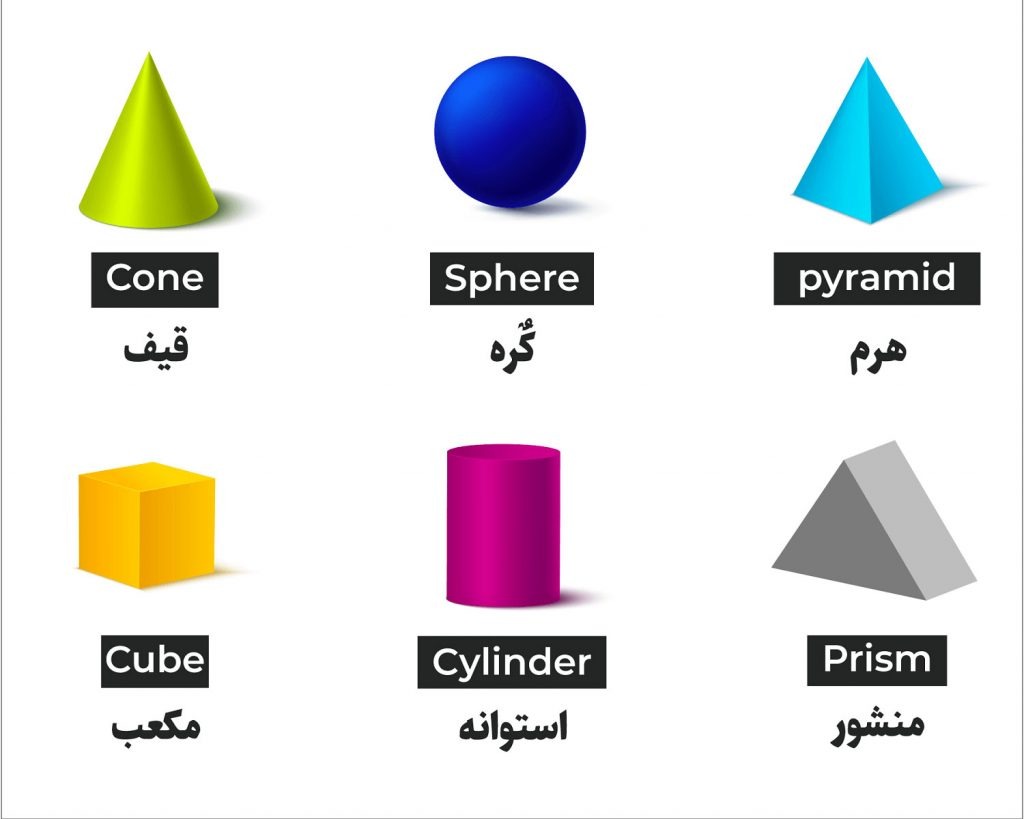
🔵 استوانه (Cylinder) – فرمولهای محاسبه
📌 تعریف و ویژگیهای کلیدی
استوانه یک شکل سهبعدی با این مشخصات است:
- دارای دو قاعده دایرهای موازی و هماندازه
- یک سطح جانبی منحنی
- ارتفاع (h): فاصله بین دو قاعده
- شعاع (r): فاصله مرکز تا لبه قاعده
🧮 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| حجم | مساحت قاعده × ارتفاع | V = πr²h |
| مساحت جانبی | محیط قاعده × ارتفاع | Aₗ = 2πrh |
| مساحت کل | (۲ × مساحت قاعده) + مساحت جانبی | Aₜ = 2πr² + 2πrh |
| مساحت قاعده | π × شعاع² | Aₚ = πr² |
🔢 مثال محاسباتی
استوانه با:
- شعاع = ۴cm
- ارتفاع = ۱۰cm
حجم = ۳.۱۴ × ۴² × ۱۰ ≈ ۵۰۲.۴ cm³
مساحت جانبی = ۲ × ۳.۱۴ × ۴ × ۱۰ ≈ ۲۵۱.۲ cm²
مساحت کل = (۲ × ۳.۱۴ × ۴²) + ۲۵۱.۲ ≈ ۳۵۱.۶۸ cm²📐 اجزای استوانه
- قاعده: دو دایره مساوی در بالا و پایین
- سطح جانبی: قسمت منحنی شکل
- محور: خط مستقیم connecting مرکز دو قاعده
💡 نکات کاربردی
- حجم استوانه معادل حجم منشور با قاعده دایرهای است
- اگر استوانه را باز کنیم، به یک مستطیل (سطح جانبی) و دو دایره تبدیل میشود
- در محاسبات:
- از مقدار π ≈ ۳.۱۴ یا ۲۲/۷ استفاده کنید
- دقت کنید واحدهای شعاع و ارتفاع یکسان باشند
📊 مقایسه با منشور
| ویژگی | استوانه | منشور |
|---|---|---|
| قاعده | دایره | چندضلعی |
| سطح جانبی | منحنی | مسطح |
| حجم | πr²h | مساحت قاعده × ارتفاع |
🔵 کره (Sphere)
📌 تعریف و ویژگیهای کلیدی
کره کاملترین شکل سهبعدی با این ویژگیهاست:
- تمام نقاط سطح آن از مرکز فاصلهای یکسان دارند
- دارای یک سطح کاملاً منحنی بدون لبه
- در طبیعت: حباب، توپ، سیارات
🧮 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| مساحت سطح | 4 × π × شعاع² | A = 4πr² |
| حجم | (4/3) × π × شعاع³ | V = (4/3)πr³ |
| قطر | 2 × شعاع | d = 2r |
🔢 مثال محاسباتی
کره با شعاع 5cm:
مساحت سطح = 4 × 3.14 × 5² ≈ 314 cm²
حجم = (4/3) × 3.14 × 5³ ≈ 523.33 cm³◻️ مکعبمستطیل (Rectangular Prism)
📌 تعریف و ویژگیها
مکعبمستطیل دارای:
- 6 وجه مستطیلی
- 12 یال
- 8 رأس
- حالت خاص: مکعب (تمام ابعاد برابر)
🧮 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| حجم | طول × عرض × ارتفاع | V = l × w × h |
| مساحت سطح | 2(lw + lh + wh) | A = 2(lw+lh+wh) |
| قطر فضایی | √(طول²+عرض²+ارتفاع²) | d = √(l²+w²+h²) |
🔢 مثال محاسباتی
مکعبمستطیل با ابعاد 3cm × 4cm × 5cm:
حجم = 3 × 4 × 5 = 60 cm³
مساحت سطح = 2(3×4 + 3×5 + 4×5) = 94 cm²📊 مقایسه کره و مکعبمستطیل
| ویژگی | کره | مکعبمستطیل |
|---|---|---|
| سطح | منحنی کامل | صفحات تخت |
| تقارن | نامتناهی | محدود |
| حجم نسبت به سطح | بهینهترین | کمتر بهینه |
💡 نکات کاربردی
- کره کمترین سطح را نسبت به حجم دارد (بهینهترین شکل)
- در مکعبمستطیل:
- تمام زوایا 90 درجه
- قطرهای هر وجه با فرمول فیثاغورث محاسبه میشوند
- عدد π ≈ 3.14159
4. مکعب (Cube)
📌 تعریف و ویژگیها
- شش وجه مربعی یکسان
- دوازده یال با طول برابر
- هشت رأس
- تمام زوایا ۹۰ درجه
- حالت خاصی از مکعبمستطیل
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| حجم | ضلع × ضلع × ضلع | V = a³ |
| مساحت سطح | ۶ × مساحت یک وجه | A = 6a² |
| قطر فضایی | a√۳ | d = a√3 |
🔢 مثال:
مکعب با ضلع ۴cm:
حجم = ۴ × ۴ × ۴ = ۶۴ cm³
مساحت سطح = ۶ × (۴ × ۴) = ۹۶ cm²5. هرم (Pyramid)
📌 تعریف و ویژگیها
- یک قاعده چندضلعی
- وجوه جانبی مثلثی
- رأس (نقطه اوج)
- ارتفاع: فاصله رأس تا قاعده
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| حجم | (مساحت قاعده × ارتفاع)/۳ | V = (Aₚ × h)/۳ |
| مساحت سطح | مساحت قاعده + مساحت وجوه جانبی | A = Aₚ + Aₗ |
🔢 مثال:
هرم مربعی با:
- ضلع قاعده = ۶cm
- ارتفاع = ۸cm
- ارتفاع وجه جانبی = ۱۰cm
حجم = (۶ × ۶ × ۸)/۳ = ۹۶ cm³
مساحت سطح = (۶ × ۶) + ۴ × (½ × ۶ × ۱۰) = ۱۵۶ cm²6. منشور (Prism)
📌 تعریف و ویژگیها
- دو قاعده همشکل و موازی
- وجوه جانبی مستطیلی
- ارتفاع: فاصله بین دو قاعده
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| حجم | مساحت قاعده × ارتفاع | V = Aₚ × h |
| مساحت سطح | (۲ × مساحت قاعده) + مساحت جانبی | A = ۲Aₚ + Aₗ |
🔢 مثال:
منشور مثلثی با:
- مساحت قاعده = ۱۲cm²
- محیط قاعده = ۱۸cm
- ارتفاع = ۷cm
حجم = ۱۲ × ۷ = ۸۴ cm³
مساحت سطح = (۲ × ۱۲) + (۱۸ × ۷) = ۱۵۰ cm²📊 جدول مقایسهای
| ویژگی | مکعب | هرم | منشور |
|---|---|---|---|
| قاعده | مربع | چندضلعی | چندضلعی |
| وجوه | ۶ مربع | ۱ چندضلعی + n مثلث | ۲ چندضلعی + n مستطیل |
| حجم | a³ | (Aₚh)/۳ | Aₚh |
🎨 [تصویر سهبعدی از مکعب، هرم و منشور]
💡 نکات کاربردی:
- در هرم، ارتفاع وجه با ارتفاع خود هرم متفاوت است
- منشورها بر اساس شکل قاعده نامگذاری میشوند
- مکعب کاملترین شکل از نظر تقارن است
🔺 مخروط (Cone) – راهنمای جامع محاسبات
📌 تعریف و خصوصیات اصلی
مخروط یک شکل سهبعدی با این ویژگیهاست:
- یک قاعده دایرهای مسطح
- یک رأس (نقطه تیز)
- یک سطح جانبی منحنی
- ارتفاع (h): فاصله عمودی رأس تا قاعده
- شعاع قاعده (r): فاصله مرکز تا لبه دایره
- ساز (s): فاصله رأس تا لبه قاعده (ارتفاع سطح جانبی)
🧮 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| حجم | (مساحت قاعده × ارتفاع)/۳ | V = (πr²h)/۳ |
| مساحت جانبی | π × شعاع × ساز | Aₗ = πrs |
| مساحت کل | مساحت قاعده + مساحت جانبی | Aₜ = πr² + πrs |
| مساحت قاعده | π × شعاع² | Aₚ = πr² |
| رابطه ساز | √(شعاع² + ارتفاع²) | s = √(r² + h²) |
🔢 مثال محاسباتی
مخروط با:
- شعاع = ۳cm
- ارتفاع = ۴cm
ساز (s) = √(۳² + ۴²) = ۵cm
حجم = (۳.۱۴ × ۳² × ۴)/۳ ≈ ۳۷.۶۸ cm³
مساحت جانبی = ۳.۱۴ × ۳ × ۵ ≈ ۴۷.۱ cm²
مساحت کل = (۳.۱۴ × ۳²) + ۴۷.۱ ≈ ۷۵.۳۶ cm²📐 انواع مخروط
- مخروط قائم:
- محور مخروط عمود بر قاعده
- رأس دقیقاً بالای مرکز دایره قرار دارد
- سازها همطول هستند
- مخروط مایل:
- محور مخروط کج است
- رأس خارج از مرکز قرار دارد
- سازها طولهای متفاوت دارند
- شعاع قاعده (r)
- ارتفاع (h)
- ساز (s)
- محور مخروط]
💡 نکات کاربردی
- حجم مخروط یکسوم استوانه با همان قاعده و ارتفاع است
- اگر مخروط را باز کنیم، به یک قطاع دایره (سطح جانبی) و یک دایره (قاعده) تبدیل میشود
- در محاسبات:
- ابتدا ساز (s) را محاسبه کنید
- از مقدار π ≈ ۳.۱۴ استفاده نمایید
- دقت کنید واحدهای شعاع و ارتفاع یکسان باشند
📊 مقایسه با هرم
| ویژگی | مخروط | هرم |
|---|---|---|
| قاعده | دایره | چندضلعی |
| سطح جانبی | منحنی | مثلثی |
| حجم | (πr²h)/۳ | (Aₚh)/۳ |
🔍 کاربردهای عملی:
- طراحی قیفهای صنعتی
- محاسبه حجم بستنی قیفی
- در معماری: گنبدها، برجها
- در طبیعت: آتشفشانها، مخروط کاج