محیط و مساحت تمام اشکال هندسی
🔍 مقدمه
هندسه یکی از شاخههای اصلی ریاضیات است که به مطالعه اشکال و ویژگیهای فضایی میپردازد. در این مقاله به بررسی محیط (اندازه دور شکل) و مساحت (اندازه سطح شکل) میپردازیم.محیط و مساحت اشکال هندسی در مبحث هندسه است و هندسه خود زیر مجموعه درس ریاضیات میباشد .
✨ مفاهیم پایه
- نقطه: موقعیتی در فضا بدون ابعاد. و تنها یک موقعیت در محور مختصات است.
- خط: یک بعدی (فقط طول) و عرض معنا ندارد
- صفحه: دو بعدی (طول و عرض) . بر روی صفحه ای تخت و بدون ضخامت قرار می گیرند .
- جسم فضایی: سه بعدی (طول، عرض و ارتفاع)
در این درس به مباحث و موضوعات زیر پرداخته میشود .
- تعریف اشکال هندسی
- محیط اشکال هندسی
- مساحت اشکال هندسی
- حجم اشکال
نکته : در فرمول های زیر * نماد ضرب و / نماد تفسیم است
📌 نمادهای ریاضی
| نماد | معنی |
|---|---|
| × | ضرب |
| ÷ | تقسیم |
| π | عدد پی (~3.14) |
انواع اشکال هندسی
- اشکال هندسی دوبعدی یا مسطح
- اشکال هندسی سه بعدی یا فضایی
🔷 اشکال هندسی دو بعدی
🔄 تفاوت با اشکال سه بعدی
- اشکال 2D ضخامت ندارند
- اشکال 3D دارای حجم هستند
- محاسبات اشکال 2D سادهتر است
📌 تعریف اشکال هندسی دو بعدی
اشکال دو بعدی به اشکالی گفته میشود که فقط طول و عرض دارند و میتوان آنها را بر روی یک صفحه تخت (بدون ضخامت) نمایش داد.
🔷 انواع اشکال هندسی
| نوع شکل | ابعاد | مثالها |
|---|---|---|
| مسطح | 2 بعدی | مربع، دایره، مثلث |
| فضایی | 3 بعدی | مکعب، کره، استوانه |
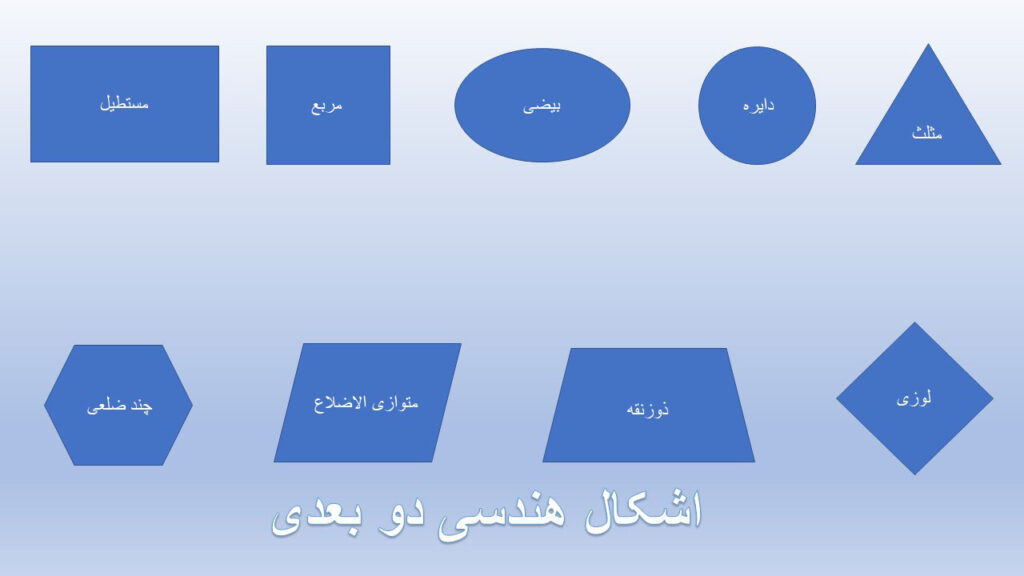
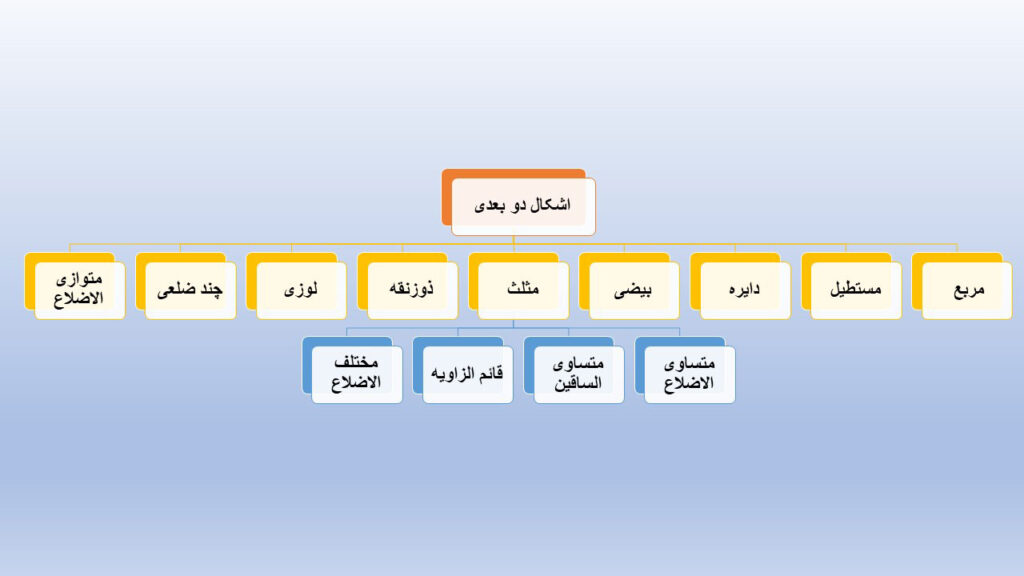
اشکال هندسی دو بعدی شامل موارد زیر هستند :
- مربع
- مستطیل
- دایره
- بیضی
- مثلث
- ذوزنقه
- لوزی
- متوازی الاضلاع
- چند ضلعی
📐 تعریف مساحت و محیط اشکال هندسی
محیط چیست ؟
محیط به اندازه دور و اطراف اشکال هندسی گفته میشود .
مساحت چیست ؟
مساحت به اندازه درون و ناحیه داخل اشکال گفته میشود .
📐 تفاوت مساحت و محیط اشکال هندسی
- محیط: اندازه دور شکل (یک بعدی)
- مساحت: اندازه سطح شکل (دو بعدی)
📏 تعاریف پایه
| مفهوم | تعریف | واحد اندازهگیری |
|---|---|---|
| محیط | اندازه کل دور یک شکل | واحد طول (سانتیمتر، متر) |
| مساحت | اندازه سطح داخل شکل | واحد سطح (سانتیمتر مربع، متر مربع) |
🎨 [تصویر اشکال هندسی دو بعدی با نام هر شکل]
نکته مهم: تمام اشکال دو بعدی را میتوان با مختصات دکارتی (x,y) در صفحه نمایش داد.
📐 محیط و مساحت اشکال هندسی دو بعدی
🔷 مربع
📌 تعریف:
چهارضلعی با چهار ضلع برابر و چهار زاویه ۹۰ درجه
🎯 ویژگیها:
- قطرها برابر و عمود بر هم
- دارای ۴ محور تقارن
📏 فرمولها:
مساحت = ضلع × ضلع → A = a²
محیط = ۴ × ضلع → P = 4a🔢 مثال:
مربعی با ضلع ۵ سانتیمتر:
مساحت = ۵ × ۵ = ۲۵ cm²
محیط = ۴ × ۵ = ۲۰ cm🔶 مستطیل
📌 تعریف:
چهارضلعی با دو جفت ضلع برابر و زوایای ۹۰ درجه
🎯 ویژگیها:
- قطرها برابر
- دارای ۲ محور تقارن
📏 فرمولها:
مساحت = طول × عرض → A = l × w
محیط = ۲ × (طول + عرض) → P = 2(l + w)🔢 مثال:
مستطیل با ابعاد ۶×۴ سانتیمتر:
مساحت = ۶ × ۴ = ۲۴ cm²
محیط = ۲ × (۶ + ۴) = ۲۰ cm🔵 دایره
📌 تعریف:
مجموعه نقاط با فاصله یکسان از مرکز
🎯 اجزا:
- شعاع (r): فاصله مرکز تا محیط
- قطر (d): ۲r
📏 فرمولها:
محیط = ۲πr یا πd → C = 2πr
مساحت = πr² → A = πr²🔢 مثال:
دایره با شعاع ۳ سانتیمتر (π≈3.14):
محیط = ۲ × 3.14 × ۳ ≈ ۱۸.۸۴ cm
مساحت = 3.14 × ۳² ≈ ۲۸.۲۶ cm²📊 جدول مقایسهای
| شکل | محیط | مساحت |
|---|---|---|
| مربع | 4a | a² |
| مستطیل | 2(l+w) | l×w |
| دایره | 2πr | πr² |
🎨 [تصویر مقایسهای اشکال با فرمولها]
💡 نکات طلایی:
- در دایره، قطر همیشه دو برابر شعاع است (d=2r)
- مربع نوع خاصی از مستطیل است که همه اضلاعش برابرند
- عدد π (پی) تقریباً برابر 3.14 یا 22/7 است
🔵 بیضی (Ellipse)
📌 تعریف و ویژگیها
بیضی یک منحنی بسته و متقارن است که:
- دارای دو قطر اصلی با اندازههای مختلف
- قطر بزرگ (Major Axis): بلندترین قطر
- قطر کوچک (Minor Axis): کوتاهترین قطر
- دو کانون (Foci) دارد که مجموع فاصله هر نقطه روی بیضی تا این دو کانون ثابت است
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| مساحت | π × (نصف قطر بزرگ) × (نصف قطر کوچک) | A = π × a × b |
| محیط (تقریبی) | π × [3(a + b) – √((3a + b)(a + 3b))] | – |
🔢 مثال محاسبه مساحت:
بیضی با:
- قطر بزرگ (2a) = 10cm → a = 5cm
- قطر کوچک (2b) = 6cm → b = 3cm
مساحت = 3.14 × 5 × 3 ≈ 47.1 cm²🎯 نکات مهم:
- a همیشه نشاندهنده نصف قطر بزرگتر است
- b نشاندهنده نصف قطر کوچکتر است
- اگر a = b باشد، بیضی تبدیل به دایره میشود
- فرمول محیط بیضی تقریبی است (محاسبه دقیق نیاز به انتگرال دارد)
📊 مقایسه با دایره
| ویژگی | دایره | بیضی |
|---|---|---|
| تقارن | کامل | دو محوری |
| قطرها | برابر | نابرابر |
| کانون | یک نقطه | دو نقطه |
💡 کاربردها:
- مدار سیارات (بیضیشکل)
- طراحی لنزها و آینهها
- معماری و طراحی صنعتی
🔺 مثلث: انواع و فرمولهای محاسبه
📌 تعریف مثلث
مثلث یک شکل هندسی سهضلعی و مسطح است که:
- از سه ضلع صاف تشکیل شده
- سه زاویه داخلی دارد
- مجموع زوایای داخلی آن همیشه ۱۸۰ درجه است
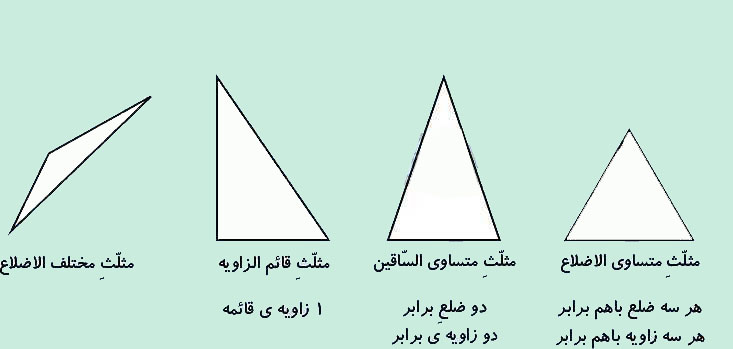
🔷 انواع مثلث
۱. مثلث متساویالاضلاع
- ویژگیها:
- سه ضلع برابر
- سه زاویه ۶۰ درجه
- سه محور تقارن
- فرمولها:
- محیط: P = 3a
- مساحت: A = (√3/4)a² یا (قاعده × ارتفاع)/۲
۲. مثلث متساویالساقین
- ویژگیها:
- دو ضلع برابر
- دو زاویه برابر
- یک محور تقارن
- فرمولها:
- محیط: P = 2a + b
- مساحت: A = (قاعده × ارتفاع)/۲
۳. مثلث قائمالزاویه
- ویژگیها:
- یک زاویه ۹۰ درجه
- وتر (بلندترین ضلع)
- دو ساق (اضلاع کوتاهتر)
- رابطه فیثاغورث: c² = a² + b²
- فرمولها:
- مساحت: A = (ساق × ساق)/۲
- محیط: P = a + b + c
۴. مثلث مختلفالاضلاع
- ویژگیها:
- سه ضلع نابرابر
- سه زاویه نابرابر
- بدون محور تقارن
- فرمولها:
- محیط: P = a + b + c
- مساحت: A = (قاعده × ارتفاع)/۲
📏 فرمولهای کلی مثلث
| پارامتر | فرمول | نمادها |
|---|---|---|
| محیط | مجموع سه ضلع | P = a + b + c |
| مساحت | (قاعده × ارتفاع)/۲ | A = (b × h)/۲ |
| قانون هرون | √[s(s-a)(s-b)(s-c)] | s = نصف محیط |
🔢 مثالهای محاسباتی
مثال ۱ (متساویالاضلاع):
- ضلع = ۶cm
- ارتفاع ≈ ۵.۲cm
محیط = ۳ × ۶ = ۱۸cm
مساحت = (۶ × ۵.۲)/۲ ≈ ۱۵.۶cm²مثال ۲ (قائمالزاویه):
- ساقها: ۳cm و ۴cm
- وتر = ۵cm (با فیثاغورث)
مساحت = (۳ × ۴)/۲ = ۶cm²
محیط = ۳ + ۴ + ۵ = ۱۲cm📊 جدول مقایسهای
| نوع مثلث | اضلاع | زوایا | تقارن |
|---|---|---|---|
| متساویالاضلاع | سه ضلع برابر | سه زاویه ۶۰° | ۳ محور |
| متساویالساقین | دو ضلع برابر | دو زاویه برابر | ۱ محور |
| قائمالزاویه | یک زاویه ۹۰° | – | – |
| مختلفالاضلاع | سه ضلع نابرابر | سه زاویه نابرابر | بدون تقارن |
🎨 [تصویر انواع مثلث با مشخصات]
💡 نکات کاربردی:
- در مثلث قائمالزاویه، ارتفاع همان ساق عمود بر قاعده است
- برای محاسبه مساحت مثلث مختلفالاضلاع، قانون هرون دقیقتر است
- مثلث متساویالاضلاع حالت خاصی از متساویالساقین است
🔷 ذوزنقه (Trapezoid)
📌 تعریف و ویژگیها
ذوزنقه چهارضلعی است که:
- فقط دو ضلع موازی دارد (قاعده بزرگ و کوچک)
- دو ضلع غیرموازی را ساقهای ذوزنقه مینامند
- ارتفاع: فاصله عمودی بین دو قاعده موازی
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| مساحت | ½ × ارتفاع × (قاعده بزرگ + قاعده کوچک) | A = ½h(a+b) |
| محیط | مجموع چهار ضلع | P = a+b+c+d |
🔢 مثال محاسبه:
ذوزنقه با:
- قاعده بزرگ (a) = 8cm
- قاعده کوچک (b) = 5cm
- ارتفاع (h) = 4cm
- ساقها (c,d) = 3cm و 4cm
مساحت = ½ × 4 × (8+5) = 26cm²
محیط = 8+5+3+4 = 20cm🎯 انواع ذوزنقه
- ذوزنقه متساویالساقین:
- ساقهای برابر
- زوایای مجاور هر قاعده برابر
- ذوزنقه قائمالزاویه:
- یک زاویه 90 درجه
- ذوزنقه مختلفالاضلاع:
- ساقهای نابرابر
🔶 لوزی (Rhombus)
📌 تعریف و ویژگیها
لوزی چهارضلعی است که:
- چهار ضلع برابر دارد
- اضلاع مقابل موازیند
- قطرها عمود بر هم و یکدیگر را نصف میکنند
- زوایای مقابل برابرند
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| مساحت | ½ × حاصلضرب قطرها | A = ½(d₁×d₂) |
| محیط | 4 × طول یک ضلع | P = 4a |
🔢 مثال محاسبه:
لوزی با:
- قطرها = 6cm و 8cm
- ضلع = 5cm
مساحت = ½ × 6 × 8 = 24cm²
محیط = 4 × 5 = 20cm💡 نکات ویژه
- مربع نوع خاصی از لوزی است که زوایای قائمه دارد
- هر لوزی یک متوازیالاضلاع است
- قطرهای لوزی نیمساز زوایای آن هستند
📊 جدول مقایسهای
| ویژگی | ذوزنقه | لوزی |
|---|---|---|
| اضلاع موازی | 2 ضلع | 2 جفت |
| تمام اضلاع | نابرابر | برابر |
| قطرها | – | عمود منصف |
| تقارن | محدود | 2 محور |
🎨 [تصویر ذوزنقه و لوزی با مشخصات]
🔍 کاربردها:
- طراحی جواهرات (لوزی)
- معماری سقفها (ذوزنقه)
- علائم راهنمایی و رانندگی
🔷 متوازیالاضلاع (Parallelogram)
📌 تعریف و ویژگیهای کلیدی
متوازیالاضلاع چهارضلعی با این ویژگیهاست:
- اضلاع مقابل موازی و همطول
- زوایای مقابل برابر
- قطرها یکدیگر را نصف میکنند
- مجموع زوایای مجاور ۱۸۰ درجه
🔶 انواع خاص
- مربع:
- تمام اضلاع و زوایا برابر
- قطرها برابر و عمود
- مستطیل:
- زوایای ۹۰ درجه
- قطرها برابر
- لوزی:
- تمام اضلاع برابر
- قطرها عمود
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| مساحت | قاعده × ارتفاع | A = b × h |
| محیط | ۲ × (ضلع۱ + ضلع۲) | P = 2(a + b) |
🔢 مثال:
متوازیالاضلاع با:
- قاعده = ۶cm
- ارتفاع = ۴cm
- ضلع مجاور = ۵cm
مساحت = ۶ × ۴ = ۲۴cm²
محیط = ۲ × (۶ + ۵) = ۲۲cm🔶 چندضلعیهای منتظم (Regular Polygons)
📌 تعریف و ویژگیها
چندضلعیای که:
- تمام اضلاع و زوایا برابر
- متقارن محوری و مرکزی
- دارای آپوتم (فاصله مرکز تا ضلع)
🔢 انواع رایج
| نام | تعداد اضلاع |
|---|---|
| مثلث متساویالاضلاع | ۳ |
| مربع | ۴ |
| پنجضلعی منتظم | ۵ |
| ششضلعی منتظم | ۶ |
📏 فرمولهای محاسبه
| پارامتر | فرمول | نمادها |
|---|---|---|
| محیط | تعداد اضلاع × طول ضلع | P = n × s |
| مساحت | (محیط × آپوتم)/۲ | A = (P × a)/۲ |
مثال:
ششضلعی منتظم با:
- ضلع = ۵cm
- آپوتم ≈ ۴.۳۳cm
محیط = ۶ × ۵ = ۳۰cm
مساحت = (۳۰ × ۴.۳۳)/۲ ≈ ۶۵cm²📊 مقایسه اشکال
| ویژگی | متوازیالاضلاع | چندضلعی منتظم |
|---|---|---|
| اضلاع | دو جفت برابر | همه برابر |
| زوایا | دو جفت برابر | همه برابر |
| تقارن | مرکزی | محوری+مرکزی |
🎨 [تصویر دیاگرام اشکال با فرمولها]
💡 نکات طلایی:
- هر مستطیل، مربع و لوزی متوازیالاضلاع است
- در چندضلعیها، هرچه تعداد اضلاع بیشتر شود به دایره نزدیکتر میشود
- آپوتم با فرمول a = s/(2tan(180°/n)) محاسبه میشود
ادامه محیط و مساحت اشکال هندسی ( سه بعدی یا فضایی )